عدد e (نپر)
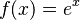 در نقطهٔ
در نقطهٔ  برابر
برابر  شود. از این طریق تابع
شود. از این طریق تابع 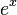 به عنوان تابع نمایی و تابع معکوس آن، به عنوان تابع لگاریتم طبیعی یا لگاریتم در مبنای
به عنوان تابع نمایی و تابع معکوس آن، به عنوان تابع لگاریتم طبیعی یا لگاریتم در مبنای  معرفی میشود. از طرفی میتوان
معرفی میشود. از طرفی میتوان  را به عنوان مبنای تابع لگاریتم طبیعی(با استفاده از انتگرال)، به عنوان حد یک دنباله ریاضی و یا به عنوان حد یک سری ریاضی تعریف کرد.
را به عنوان مبنای تابع لگاریتم طبیعی(با استفاده از انتگرال)، به عنوان حد یک دنباله ریاضی و یا به عنوان حد یک سری ریاضی تعریف کرد.
گاهی عدد  ، به افتخار ریاضیدان سوئیسی، لئونارد اویلر (به آلمانی: Leonhard Euler)، عدد اویلر نامیده میشود. همچنین گاهی نیز از آن به اسم ثابت نپر (جان نپر (به انگلیسی: John Napier)) یاد میشود، با این حال نماد
، به افتخار ریاضیدان سوئیسی، لئونارد اویلر (به آلمانی: Leonhard Euler)، عدد اویلر نامیده میشود. همچنین گاهی نیز از آن به اسم ثابت نپر (جان نپر (به انگلیسی: John Napier)) یاد میشود، با این حال نماد  به افتخار اویلر انتخاب شدهاست.
به افتخار اویلر انتخاب شدهاست.
در ریاضیات عدد  در کنار عدد ۰، عدد ۱، عدد پی (به یونانی: π) و عدد یکه موهومی
در کنار عدد ۰، عدد ۱، عدد پی (به یونانی: π) و عدد یکه موهومی  از معروفیت خاصی در ریاضی برخوردار است. علاوه بر تعریف انتزاعی آنها، این پنج عدد نقش مهم و کلیدیی در سرتاسر ریاضیات بازی میکنند. برای مثال میتوان هر پنج عدد را در معادلهٔ مشخصهٔ اویلر مشاهده کرد.
از معروفیت خاصی در ریاضی برخوردار است. علاوه بر تعریف انتزاعی آنها، این پنج عدد نقش مهم و کلیدیی در سرتاسر ریاضیات بازی میکنند. برای مثال میتوان هر پنج عدد را در معادلهٔ مشخصهٔ اویلر مشاهده کرد.
عدد  یک عدد گنگ است؛ یعنی این عدد، کسری از اعداد صحیح نیست. به علاوه، این عدد یک عدد متعالی است؛ یعنی نمیتواند ریشهٔ هیچ معادلهٔ چند جملهای غیر صفر با ضرایب گویا باشد. عدد
یک عدد گنگ است؛ یعنی این عدد، کسری از اعداد صحیح نیست. به علاوه، این عدد یک عدد متعالی است؛ یعنی نمیتواند ریشهٔ هیچ معادلهٔ چند جملهای غیر صفر با ضرایب گویا باشد. عدد  تا ۵۰ رقم اعشار مطابق عدد زیر است:
تا ۵۰ رقم اعشار مطابق عدد زیر است:
۲٫۷۱۸۲۸۱۸۲۸۴۵۹۰۴۵۲۳۵۳۶۰۲۸۷۴۷۱۳۵۲۶۶۲۴۹۷۷۵۷۲۴۷۰۹۳۶۹۹۹۵..
به ادامه مطلب بروید.